Rossler Solution with delay
function dde_rossler
% 延迟Rossler系统(1)
%
% 方程如下:
% dx/dt=-y-z+k*(x(t-tau)-x)
% dy/dt=x+a*y
% dz/dt=b+z*(x-c)
%
%
% Author's email: ustb03-07@yahoo.com.cn
%
history = [-4;4;0];
tspan = [0,250];
opts = ddeset('RelTol',1e-5,'AbsTol',1e-8);
a = 0.2;
b = 0.2;
c = 4.5;
% 一周期
k = 0.2;
% 二周期
% k = 0.08;
% Solve the DDEs that arise when there is a delay of tau.
tau = 5.691;
sol = dde23(@dde_rosslerf,tau,history,tspan,opts,a,b,c,k);
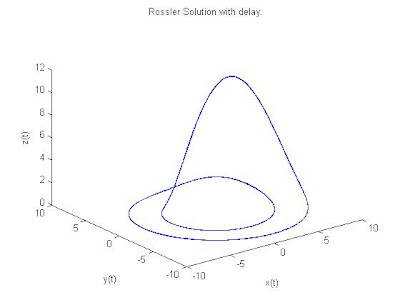
plot3(sol.y(1,4000:end),sol.y(2,4000:end),sol.y(3,4000:end))
title('Rossler Solution with delay.')
xlabel('x(t)')
ylabel('y(t)')
zlabel('z(t)')
%--------------------------
function dydt = dde_rosslerf(t,y,Z,a,b,c,k)
% Differential equations function for Rossler.
ylag = Z(:,1);
dydt = [ -y(2)-y(3)+k*(ylag(1)-y(1))
y(1)+a*y(2)
b+y(1)*y(3)-c*y(3) ];
function dde_rossler2
% 延迟Rossler系统(2)
%
% 方程如下:
% dx/dt=-y-z
% dy/dt=x+a*y+k*(x(t-tau)-x)
% dz/dt=b+z*(x-c)
%
%
% Author's email: ustb03-07@yahoo.com.cn
%
history = [-4;4;0];
tspan = [0,200];
opts = ddeset('RelTol',1e-5,'AbsTol',1e-8);
a = 0.2;
b = 0.2;
c = 5.7;
% Solve the DDEs that arise when there is a delay of tau.
k = 0.025;
tau = 17.4;
sol = dde23(@dde_rosslerf,tau,history,tspan,opts,a,b,c,k);
plot3(sol.y(1,3000:end),sol.y(2,3000:end),sol.y(3,3000:end))
title('Rossler Solution with delay.')
xlabel('x(t)')
ylabel('y(t)')
zlabel('z(t)')
%--------------------------
function dydt = dde_rosslerf(t,y,Z,a,b,c,k)
% Differential equations function for Rossler.
ylag = Z(:,1);
dydt = [ -y(2)-y(3)
y(1)+a*y(2)+k*(ylag(1)-y(1))
b+y(1)*y(3)-c*y(3) ];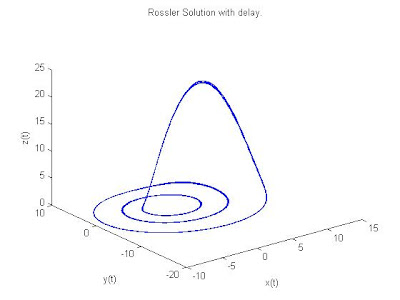
1 comment:
收下了。:)
Post a Comment