Josephon系统(Poincare图象和Lyapunov指数)
Josephon.m
function dx=Josephon(t,x);
% Josephon方程
% dx=Josephon(t,[x;y;b])
% t-时间,x,y-为自变量,b-为如下方程所示的参数
% eg: dx=Josephon(10,[0;0;.33803])
%
% 方程如下:
% θ''+G*θ'+sinθ=I+A*sin(ωt)+αsin(βωt)
% 变化:
% dx=y
% dy=-G*y-sin(x)+I+A*sin(w*t)+a*sin(b*w*t)
%
% Example(Poincare图象):
% [T,Y]=ode45('Josephon',[0,1000],[0;0;.33803]);
% plot(mod(Y(:,1),6.283),Y(:,2),'.','markersize',2);
%
% Author's email: ustb03-07@yahoo.com.cn
%
G=.7;A=.4;w=.25;
a=0.0125;I=.905;
% b=.33803;
b=x(3);
dx(1,1)=x(2);
dx(2,1)=-G*x(2)-sin(x(1))+I+A*sin(w*t)+a*sin(b*w*t);
dx(3,1)=0;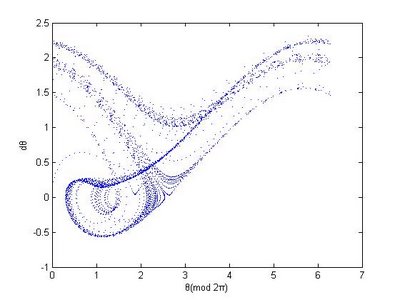
jose_ly.m
function ly=jose_ly(b,k)
% the largest lyapunov exponent of josephson
% k 迭代步数,b 参数
% 方程如下:
% θ''+G*θ'+sinθ=I+A*sin(ωt)+αsin(βωt)
% 变化:
% dx=y
% dy=-G*y-sin(x)+I+A*sin(w*t)+a*sin(b*w*t)
%
% Example:
% ly=jose_ly(0,800)
%
% Author:LDYU
% Author's email: ustb03-07@yahoo.com.cn
%
d0=1e-8;
ly=0;
lsum=0;
x=[0;2;b];
x1=[d0;2;b];
for t=1:k
[T1,Y1]=ode45('Josephon',[t-1,t],x);
[T2,Y2]=ode45('Josephon',[t-1,t],x1);
x=Y1(end,:);
x1=Y2(end,:);
d1=norm(x-x1);
x1=x+(d0/d1)*(x1-x);
lsum=lsum+log(d1/d0);
end
ly=lsum/k;
>> help jose_ly
the largest lyapunov exponent of josephson
k 迭代步数,b 参数
方程如下:
θ''+G*θ'+sinθ=I+A*sin(ωt)+αsin(βωt)
变化:
dx=y
dy=-G*y-sin(x)+I+A*sin(w*t)+a*sin(b*w*t)
Example:
ly=jose_ly(0,800)
Author:LDYU
Author's email: ustb03-07@yahoo.com.cn
>> ly=jose_ly(0,800)
ly =
0.0522
josel.m
% the largest lyapunov exponents of josephson
%
% Author's email: ustb03-07@yahoo.com.cn
%
clear
Z=[];
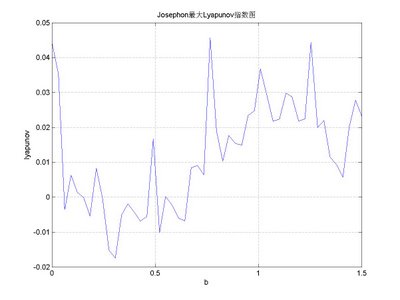
for b=linspace(0,1.5,50)
Z=[Z b+i*jose_ly(b,300)];
end
plot(Z,'-')
title('Josephon最大Lyapunov指数图'),xlabel('b'),ylabel('lyapunov')
grid on
>> josel