基于奇异值分解的Lyapunov指数计算

前几星期一个学友和我探讨了《一类基于奇异值分解的Lyapunov指数计算方法》一文
的方法，他把Henon映射的程序做出了，但Lorenz的程序却得不到正确的值。我试了
并得到了比较好的结果。现在贴出和大家分享。

henon_le.m

% 奇异值分解求Lyapunov法 % 差分henon系统 x=0.6;y=0.4; V=eye(2); S=V;b=0; k=200; for i=1:k J=[-2.8*x 0.3;1 0]; B=J*V*S; [V,S,U]=svd(B); a_max=max(diag(S)); S=(1/a_max)*S; b=b+log(a_max); x_next=1+0.3*y-1.4*x*x; y_next=x; x=x_next; y=y_next; end Lyapunov=(log(diag(S))+b)/k

Lyapunov =
 
    0.4120
   -1.6160

lorenz_euler.m

% Lorenz图形(欧拉方法) % % Author：yujunjie % Author's email: ustb03-07@yahoo.com.cn % clear h=0.006;a=16;b=4;c=49.52; x=20;y=20;z=50; Y=[]; for i=1:8000 x1=x+h*a*(y-x); y1=y+h*(c*x-x*z-y); z1=z+h*(x*y-b*z); x=x1;y=y1;z=z1; Y(i,:)=[x y z]; end plot3(Y(:,1),Y(:,2),Y(:,3));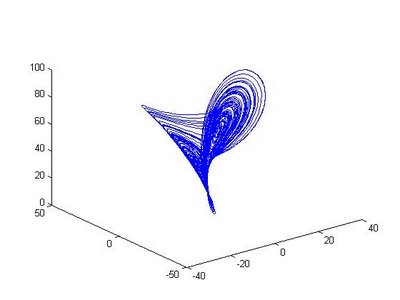

lorenz_le_eu.m

% 奇异值分解求Lyapunov法 % 微分lorenz系统 % % Author：yujunjie % Author's email: ustb03-07@yahoo.com.cn % x=20;y=20;z=50;h=0.002; a=16;b=4;c=49.52; V=eye(3); S=V;b1=0; k=4000; for i=1:k x1=x+h*a*(y-x); y1=y+h*(c*x-x*z-y); z1=z+h*(x*y-b*z); x=x1;y=y1;z=z1; J=[-a a 0 c-z -1 -x y x -b]; J=eye(3)+h*J; B=J*V*S; [V,S,U]=svd(B); a_max=max(diag(S)); S=(1/a_max)*S; b1=b1+log(a_max); end Lyapunov=(log(diag(S))+b1)/(k*h)

Lyapunov =
 
    1.5172
    0.0016
  -22.5679

lorenz_le_rk.m

% 奇异值分解求Lyapunov法 % 微分lorenz系统 % % dx/dt = SIGMA*(y - x) % dy/dt = BETA*x - y -x*z % dz/dt= x*y - GAMA*z % In this demo, SIGMA = 16,BETA = 45.92, GAMA = 4 % Initial conditions: x(0) = 1, y(0) = 1, z(0) = 1; % Reference values: % LE1 = 1.497, LE2 = 0.00, LE3 = -22.46, LD = 2.07 sigma=16;beta=45.92;gama=4; x(1)=1;y(1)=1;z(1)=1;V=diag(ones(1,3));S=V;I=V;b=0; h=0.005;k=5000; for i=1:k k11=sigma*(-x(i)+y(i)); k21=beta*x(i)-x(i)*z(i)-y(i); k31=x(i)*y(i)-gama*z(i); k12=sigma*(-(x(i)+0.5*h*k11)+(y(i)+0.5*h*k21)); k22=beta*(x(i)+0.5*h*k11)-(x(i)+0.5*h*k11)... *(z(i)+0.5*h*k31)-(y(i)+0.5*h*k21); k32=(x(i)+0.5*h*k11)*(y(i)+0.5*h*k21)-gama*(z(i)+0.5*h*k31); k13=sigma*(-(x(i)+0.5*h*k12)+(y(i)+0.5*h*k22)); k23=beta*(x(i)+0.5*h*k12)-(x(i)+0.5*h*k12)*... (z(i)+0.5*h*k32)-(y(i)+0.5*h*k22); k33=(x(i)+0.5*h*k12)*(y(i)+0.5*h*k22)-gama*(z(i)+0.5*h*k32); k14=sigma*(-(x(i)+h*k13)+(y(i)+h*k23)); k24=beta*(x(i)+h*k13)-(x(i)+h*k13)*(z(i)+h*k33)-(y(i)+h*k23); k34=(x(i)+h*k13)*(y(i)+h*k23)-gama*(z(i)+h*k33); J1=[-sigma sigma 0;beta-z(i) -1 -x(i);y(i) x(i) -gama]; J2=[-sigma sigma 0; beta-(z(i)+0.5*h*k31) -1 -(x(i)+0.5*h*k11); y(i)+0.5*h*k21 x(i)+0.5*h*k11 -gama]; J3=[-sigma sigma 0; beta-(z(i)+0.5*h*k32) -1 -(x(i)+0.5*h*k12); y(i)+0.5*h*k22 x(i)+0.5*h*k12 -gama]; J4=[-sigma sigma 0; beta-(z(i)+h*k33) -1 -(x(i)+h*k13); y(i)+h*k23 x(i)+h*k13 -gama]; J=I+h*(J1+2*J2*(I+0.5*h*J1)+2*J3*(I+0.5*h*J2*(I+0.5*h*J1))... +J4*(I+0.5*h*J3*(I+0.5*h*J2*(I+0.5*h*J1))))/6; B=J*V*S; [V,S,U]=svd(B); am=max(diag(S)); S=S/am; b=b+log(am); x(i+1)=x(i)+h*(k11+2*k12+2*k13+k14)/6; y(i+1)=y(i)+h*(k21+2*k22+2*k23+k24)/6; z(i+1)=z(i)+h*(k31+2*k32+2*k33+k34)/6; end for i=1:3 le(i)=(log(diag(S(i,i)))+b)/(k*h); end le'

    1.3452
    0.1502
  -22.5502