切分段线性控制方法2
% 连续时间系统混沌化切控制方法
% 《动力系统的混沌化》陈关荣 汪小帆
%
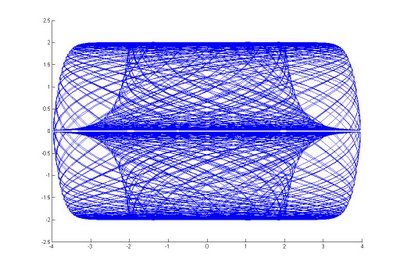
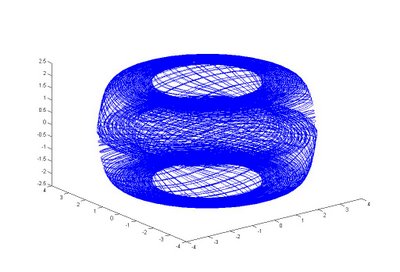
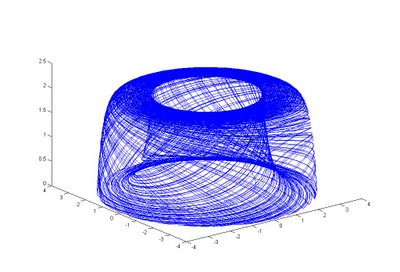
% Example(函数图象):
% [T,Y]=ode45('chaos2',40,[2;2;1]);
% plot3(Y(:,1),Y(:,2),Y(:,3));
% hold on
% [T,Y]=ode45('chaos2',40,[2;2;-1]);
% plot3(Y(:,1),Y(:,2),Y(:,3));
%
function dx=chaos2(t,x);
a=3;b=20;c=-20;
k=4;d=10;
m=4;e=-10;
A= [ a b 0
-b a 0
0 0 c];
if x(3)+norm(x(1:2))>k & x(3)>0
u=k*[-x(1) -x(2) d]';
elseif x(3)-norm(x(1:2))<-m & x(3)<0
u=m*[-x(1) -x(2) e]';
else
u=0;
end
dx=A*x+u;