Chaos Synchronization

lorenz_Synchronous.m

function lorenz_Synchronous % Lorenz 系统同步 % % Author:LDYU % Author's email: ustb03-07@yahoo.com.cn % [T,Y]=ode45(@lorenzf1,[0,3],[1;-10;1;10;2]); subplot(2,1,1) plot(T,Y(:,3),'k') hold on plot(T,Y(:,5),'b') [T,Y]=ode45(@lorenzf2,[0,3],[10;10;10;-20;2]); subplot(2,1,2) plot(T,Y(:,3),'k') hold on plot(T,Y(:,5),'b') %------------------------------------- function dx=lorenzf1(t,x) % dx= a*(y-x) % dy= -x*z+r*x-y % dz= x*y-b*z % dy1= -x*z1+r*x-y1 % dz1= x*y1-b*z1 a=16;b=4;r=45.92; dx=[ a*(x(2)-x(1)) -x(1)*x(3)+r*x(1)-x(2) x(1)*x(2)-b*x(3) -x(1)*x(5)+r*x(1)-x(4) x(1)*x(4)-b*x(5)]; %------------------------------------- function dx=lorenzf2(t,x) % dx= a*(y-x) % dy=-x*z+r*x-y % dz= x*y-b*z % dx1=a*(y-x1) % dz1=x1*y-b*z1 a=16;b=4;r=45.92; dx=[ a*(x(2)-x(1)) -x(1)*x(3)+r*x(1)-x(2) x(1)*x(2)-b*x(3) a*(x(2)-x(4)) x(4)*x(2)-b*x(5)];

用WOLF方法求时间延迟CHEN系统最大LYAPUNOV指数

wolf_3Dlyapunov.m

function lyapunov=wolf_3Dlyapunov(t,Y) % 用wolf方法求三维实验数据最大李雅普洛夫指数 % % 输入：演化时间间隔t，3维数据Y(:,1:3) % 输出：lyapunov指数 % % Author：yujunjie % Author's email: ustb03-07@yahoo.com.cn % lyapunov=0; YL=length(Y); % 不同的系统以下两个参数可能要适当的改变 MaxFL=.5; MaxEL=2.5; fiducial1=1; fiducial2=3; for i=4:YL if (sum(abs(Y(fiducial1,:)-Y(i,:)))<MaxFL) fiducial2=i; break; end end evolveStep=1; L1=norm(Y(fiducial1,:)-Y(fiducial2,:)); L2=norm(Y(fiducial1+evolveStep,:)-Y(fiducial2+evolveStep,:)); while (1) if (fiducial1+evolveStep==YL)||(fiducial2+evolveStep==YL) lyapunov=lyapunov+log(L2/L1); fiducial1=fiducial1+evolveStep; break; elseif L2>MaxEL lyapunov=lyapunov+log(L2/L1); fiducial1=fiducial1+evolveStep; fiducial2=fiducial2+evolveStep; fiducial2=findreplace(Y,fiducial1,fiducial2,MaxFL); evolveStep=1; L1=norm(Y(fiducial1,:)-Y(fiducial2,:)); else evolveStep=evolveStep+1; end L2=norm(Y(fiducial1+evolveStep,:)-Y(fiducial2+evolveStep,:)); end fiducial1=fiducial1-1; lyapunov=lyapunov/(t*fiducial1); %--------------------------------------------------- function P=findreplace(Y,P1,P2,MaxL) % 寻找替代点 P=P2; YL=length(Y); HYL=fix(YL/2); k=1; % 优先选择距离较小的,与被替代的点处于以基点为原点的坐标下相同象限中 for i=1:YL if (sum(abs(Y(P1,:)-Y(i,:))) < MaxL ... && sign(Y(P2,1)-Y(P1,1))==sign(Y(i,1)-Y(P1,1))... && sign(Y(P2,2)-Y(P1,2))==sign(Y(i,2)-Y(P1,2))... && sign(Y(P2,3)-Y(P1,3))==sign(Y(i,3)-Y(P1,3))) temp(k)=i; k=k+1; end end % 如没有满足上述条件的点不进行替代,否则取尽可能保持方向不变的点 % 此处采用取外积模最小的点 if k>1 P=temp(1); PCross=norm(cross(Y(P1,:),Y(P,:))); for i=2:k-1 PCross1=norm(cross(Y(P1,:),Y(temp(i),:))); if PCross1 < PCross P=temp(i); PCross=PCross1; end end end

取延迟Chen系统，方程如下:

+----------------------------------------+
|   dx/dt=a*(y-x)                        |
|   dy/dt=(c-a)*x+c*y-x*z+k*(y(t-tau)-y) |
|   dz/dt=x*y-b*z                        |
+----------------------------------------+ 

其中 a = 35;b = 3;c = 28;
并且 k 和 tau 取以下值时都是非混沌

k = 2.4; tau = .2;
k = 2.8; tau = .15;
k = 4.6; tau = .3;
k = 0.8; tau = .5;
k = 2.65; tau = .16;
k = 4.2; tau = .1;
k = 3.29; tau = .13;
k = 2.3; tau = .18;

见dde_chen.m

如 k=0 即为不带延迟系统
 
>> history = [-3;-4;14];
tspan = [0,50];
a = 35;b = 3;c = 28;
k = 0;tau = .3;
opts = ddeset('MaxStep',1e-2);
sol = dde23(@dde_chenf,tau,history,tspan,opts,a,b,c,k);
Y=sol.y(1:3,2000:5000);
Y=Y';
plot3(Y(:,1),Y(:,2),Y(:,3));
l=wolf_3Dlyapunov(1e-2,Y)
 
l =
 
    2.0094

==========================================

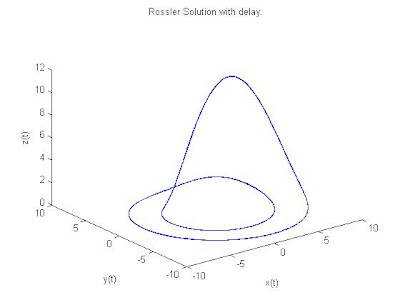
取k = 2.4;tau = .2;
 
>> history = [-3;-4;14];
tspan = [0,50];
a = 35;b = 3;c = 28;
k = 2.4;tau = .2;
opts = ddeset('MaxStep',1e-2);
sol = dde23(@dde_chenf,tau,history,tspan,opts,a,b,c,k);
Y=sol.y(1:3,2000:5000);
Y=Y';
plot3(Y(:,1),Y(:,2),Y(:,3));
l=wolf_3Dlyapunov(1e-2,Y)
 
l =
 
   -0.0969

==========================================

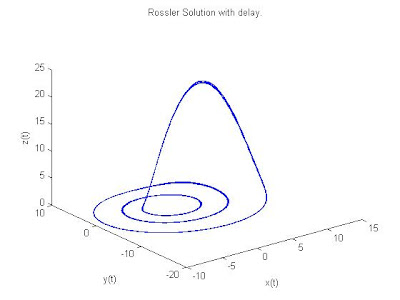
取 k = 4.2;tau = .1; 
 
>> history = [-3;-4;14];
tspan = [0,50];
a = 35;b = 3;c = 28;
k = 4.2;tau = .1;
opts = ddeset('MaxStep',1e-2);
sol = dde23(@dde_chenf,tau,history,tspan,opts,a,b,c,k);
Y=sol.y(1:3,2000:5000);
Y=Y';
plot3(Y(:,1),Y(:,2),Y(:,3));
l=wolf_3Dlyapunov(1e-2,Y)
 
l =
 
   -0.2768

==========================================

取 k = .8;tau = .6; 是混沌系统

 
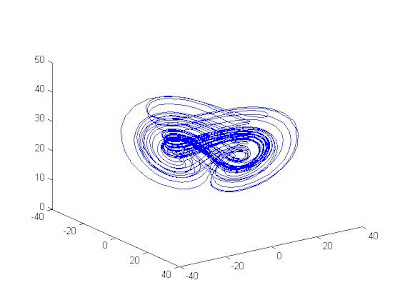
>> history = [-3;-4;14];
tspan = [0,50];
a = 35;b = 3;c = 28;
k = .8;tau = .6;
opts = ddeset('MaxStep',1e-2);
sol = dde23(@dde_chenf,tau,history,tspan,opts,a,b,c,k);
Y=sol.y(1:3,2000:5000);
Y=Y';
plot3(Y(:,1),Y(:,2),Y(:,3));
l=wolf_3Dlyapunov(1e-2,Y)
 
l =
 
    3.0002

参考程序
dde_chen.m
dde_rossler.m

参考文献：
[1]Alan WOLF,Jack B.SWIFT,Harry L.SWINNEY and John A.VASTANO DETERMINING LYAPUNOV EXPONENTS FROM A TIME SERIES Physica 16D(1985)285-317

Chen Solution with delay

function dde_chen % 延迟Chen系统 % % 方程如下: % dx/dt=a*(y-x) % dy/dt=(c-a)*x+c*y-x*z+k*(y(t-tau)-y) % dz/dt=x*y-b*z % % Author's email: ustb03-07@yahoo.com.cn % history = [-3;-4;14]; tspan = [0,25]; opts = ddeset('RelTol',1e-5,'AbsTol',1e-8); a = 35;b = 3;c = 28; k = 2.4;tau = .2; % k = 2.8;tau = .15; % k = 4.6;tau = .3; % k = .8;tau = .5; % k = 2.65;tau = .16; % k = 4.2;tau = .1; % k = 3.29;tau = .13; % k = 2.3;tau = .18; sol = dde23(@dde_chenf,tau,history,tspan,opts,a,b,c,k); plot3(sol.y(1,4000:end),sol.y(2,4000:end),sol.y(3,4000:end)) title('Chen Solution with delay.') xlabel('x(t)') ylabel('y(t)') zlabel('z(t)') %-------------------------- function dydt = dde_chenf(t,y,Z,a,b,c,k) % Differential equations function for Chen. ylag = Z(:,1); dydt = [ a*(y(2)-y(1)) (c-a-y(3))*y(1)+c*y(2)+k*(ylag(2)-y(2)) y(1)*y(2)-b*y(3) ];

Rossler Solution with delay

function dde_rossler % 延迟Rossler系统(1) % % 方程如下: % dx/dt=-y-z+k*(x(t-tau)-x) % dy/dt=x+a*y % dz/dt=b+z*(x-c) % % % Author's email: ustb03-07@yahoo.com.cn % history = [-4;4;0]; tspan = [0,250]; opts = ddeset('RelTol',1e-5,'AbsTol',1e-8); a = 0.2; b = 0.2; c = 4.5; % 一周期 k = 0.2; % 二周期 % k = 0.08; % Solve the DDEs that arise when there is a delay of tau. tau = 5.691; sol = dde23(@dde_rosslerf,tau,history,tspan,opts,a,b,c,k); plot3(sol.y(1,4000:end),sol.y(2,4000:end),sol.y(3,4000:end)) title('Rossler Solution with delay.') xlabel('x(t)') ylabel('y(t)') zlabel('z(t)') %-------------------------- function dydt = dde_rosslerf(t,y,Z,a,b,c,k) % Differential equations function for Rossler. ylag = Z(:,1); dydt = [ -y(2)-y(3)+k*(ylag(1)-y(1)) y(1)+a*y(2) b+y(1)*y(3)-c*y(3) ];

function dde_rossler2 % 延迟Rossler系统(2) % % 方程如下: % dx/dt=-y-z % dy/dt=x+a*y+k*(x(t-tau)-x) % dz/dt=b+z*(x-c) % % % Author's email: ustb03-07@yahoo.com.cn % history = [-4;4;0]; tspan = [0,200]; opts = ddeset('RelTol',1e-5,'AbsTol',1e-8); a = 0.2; b = 0.2; c = 5.7; % Solve the DDEs that arise when there is a delay of tau. k = 0.025; tau = 17.4; sol = dde23(@dde_rosslerf,tau,history,tspan,opts,a,b,c,k); plot3(sol.y(1,3000:end),sol.y(2,3000:end),sol.y(3,3000:end)) title('Rossler Solution with delay.') xlabel('x(t)') ylabel('y(t)') zlabel('z(t)') %-------------------------- function dydt = dde_rosslerf(t,y,Z,a,b,c,k) % Differential equations function for Rossler. ylag = Z(:,1); dydt = [ -y(2)-y(3) y(1)+a*y(2)+k*(ylag(1)-y(1)) b+y(1)*y(3)-c*y(3) ];